jmfriedt@ens.ens-lyon.fr
The idea of the hough transform is to look in a parameter space what
set of parameters would best fit the searched pattern in an image.
We will here consider 2 simple cases, line and circle detection.
A line is defined by 2 parameters, r and th for example if the
line equation is x.cos(th)+y.sin(th)=r. th is then the angle between
the line and the x axis while r is the distance from the line to
the origin. The parameter space in this case is (r,th) while the
'real' (image) space is (x,y). So what we want is a function
from (x,y)->(r,th) that will give us the set (r,th) that best fit
the equation of the line in the image. One way to do this would be to
look for all pair of points in the image what are the value of (r,th)
defining the line going from one point to another, add the votes
for each (r,th) pair, and take the highest vote after all the pair
of points have been considered. This method would require a huge
computational power. The approach used in the hough transform is
to consider each 'interesting' point and look at the set of curves that
could go through that point. Interesting means that a point has a
much higher value than the backgroud (if u have a black backgroud with
a white line, interesting means pixel==255 while backgroud==0).
So for each interesting point (x,y) one has the set of lines
possibly going through this point defined as r=x.cos(th)+y.sin(th)
(remember, we are now in (r,th) space while x and y are given, so
we want to draw r as a function of th). We sum all the votes (curves)
r(th) for each pair of interesting (x,y), and at the end of the algorithm,
the point in parameter space which has most votes is the set of
parameters that best defines the curve.
The same is true for circles : a circle of radius R and center (a,b)
is defined by (x-a)^2+(y-b)^2=R^2. So for a given R (because I want
my parameter space to be two dimensional while 3 parameters are
needed to define a circle), we have a=x-sqrt(R^2-(y-b)^2) (sqrt
is the square root, x and y are the coordinates of an interesting point).
Here again we get a curve in parameter space (a,b) : a=a(b) when
x,y and R are given. Again we sum all curves a(b) for each interesting (x,y)
and at the end, the point in (a,b) space which has collected most votes
is the best guess for the center coordinates of the circle we are looking for.
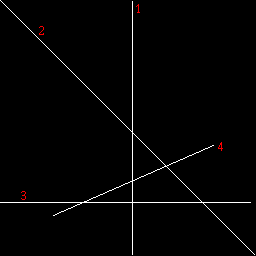
Line detection :
Parameter space is (r,th) ie angle to the x axis and distance to the center

Circle detection :
Parameter space is (a,b) coordinates of the center of the circle for R (radius
of the circle we are looking for) given. The movie at the end of the page
shows a 3D search : each frame shows the (a,b) space while time is R (ie
the radius of the circle we are looking for increases from 0 to 100 (step 2)
between each frame) :
Original image :
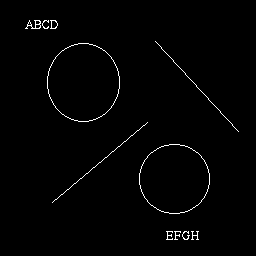
circle :

line :

Movie showing the Hough transform applied to the
search of circles (time
shows the evolution of the search for various radii) :
Readme file
C programs to perform line and
circle detection on pgm images.




